| Dec 12, 2023 |
|
(Nanowerk News) In every physical system, energy and environment interact, which is why non-Hermitian systems are common. In the context of physics and engineering, a “non-Hermitian system” refers to a situation where the interaction between energy and its environment doesn’t follow a conventional, balanced pattern. Normally, in a “Hermitian” system, things behave symmetrically, meaning the way energy moves or changes can be reversed and still make sense. This symmetry is often seen in ideal, isolated systems.
|
|
However, in a non-Hermitian system, this symmetry is broken. This happens because the energy in these systems is influenced by their environment in a way that’s not evenly balanced. For example, energy might be lost or gained in an irregular manner due to interactions with the surroundings. This concept is important because it reflects a more realistic scenario in the real world, where systems are often not perfectly isolated and are influenced by their environments in complex ways.
|
|
These systems are described by non-Hermitian Hamiltonians and come in two types: those with nonreciprocal (one-way) coupling and those with both gain and loss elements.
|
|
“Non-Hermitian Hamiltonians” describe the mathematical models used to understand the behavior of non-Hermitian systems. In physics, a Hamiltonian is a formula that encapsulates the total energy of a system, including both kinetic and potential energy. Normally, in Hermitian systems, these Hamiltonians have a special symmetry that leads to predictable, stable behaviors and real energy values.
|
|
However, in non-Hermitian systems, this symmetry is absent in the Hamiltonians. This lack of symmetry means that the energy values can be complex and the behavior of the system can be unpredictable or unstable. Non-Hermitian Hamiltonians are essential for modeling systems where energy is not conserved in the traditional sense due to interactions with the environment.
|
|
The two types mentioned – systems with nonreciprocal coupling and those with both gain and loss elements – represent different ways this energy-environment interaction can occur. Nonreciprocal coupling refers to situations where the interaction only goes one way; energy can move from one part of the system to another, but not back the other way. On the other hand, systems with gain and loss elements can both absorb energy from and release energy to their environment, leading to more complex dynamics. These concepts are crucial in understanding systems that deviate from traditional, isolated physics models, finding applications in various fields like optics, quantum mechanics, and materials science.
|
|
In 2016, three physicists received the Nobel Prize in Physics for discovering topological phases and transitions. Lately, combining topological and non-Hermitian photonics has led to new developments like topological lasers, controlling light in unique ways, and creating entangled-photon emitters. Compared to nonreciprocal coupling, it’s easier to create specific patterns of gain and loss in different systems. However, there are challenges in achieving nonreciprocal coupling between layers in these systems. Also, adding nonreciprocity to topological photonic systems can change their original topological properties.
|
|
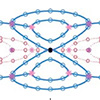
Professors Xiaoyong Hu and Qihuang Gong and their team at Peking University in China are exploring non-Hermitian topological photonics. They have proposed a way to achieve nonreciprocal coupling between layers in these systems by introducing gain/loss at specific sites in bilayer non-Hermitian topological systems. They aim to understand how two key aspects of non-Hermiticity are related and how nonreciprocal coupling and on-site gain/loss are similar in both one-dimensional and two-dimensional bilayer topological systems.
|
|
Their findings, published in Frontiers of Optoelectronics (“A scheme for realizing nonreciprocal interlayer coupling in bilayer topological systems”) could lead to new ways of studying and controlling non-Hermitian topological states in these systems. They foresee possible uses such as observing unique behaviors in three-dimensional systems and studying the physics of non-Hermitian bands.
|